6549번: 히스토그램에서 가장 큰 직사각형
사용 언어: C++
문제
히스토그램은 직사각형 여러 개가 아래쪽으로 정렬되어 있는 도형이다. 각 직사각형은 같은 너비를 가지고 있지만, 높이는 서로 다를 수도 있다. 예를 들어, 왼쪽 그림은 높이가 2, 1, 4, 5, 1, 3, 3이고 너비가 1인 직사각형으로 이루어진 히스토그램이다.
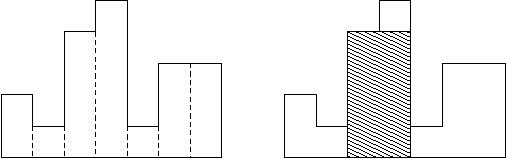
히스토그램에서 가장 넓이가 큰 직사각형을 구하는 프로그램을 작성하시오.
입력
입력은 테스트 케이스 여러 개로 이루어져 있다. 각 테스트 케이스는 한 줄로 이루어져 있고, 직사각형의 수 n이 가장 처음으로 주어진다. (1 ≤ n ≤ 100,000) 그다음 n개의 정수 h1, ..., hn (0 ≤ hi ≤ 1,000,000,000)가 주어진다. 이 숫자들은 히스토그램에 있는 직사각형의 높이이며, 왼쪽부터 오른쪽까지 순서대로 주어진다. 모든 직사각형의 너비는 1이고, 입력의 마지막 줄에는 0이 하나 주어진다.
출력
각 테스트 케이스에 대해서, 히스토그램에서 가장 넓이가 큰 직사각형의 넓이를 출력한다.
풀이
코드를 그림을 보면서 이해하고 싶으면 https://sexycoder.tistory.com/107을 한번 보는 것을 추천한다.
#include <iostream>
#include <vector>
#include <algorithm>
#include <cmath>
using namespace std;
//세그먼트 트리를 초기화할 때 해당 구간 내 가장 낮은 막대의 인덱스를 저장
void init(vector<long long> &array, vector<long long> &tree, int node, int start, int end)
{
// start 와 end 의 위치가 일치하면 start 값을 넣어준다
if(start == end)
tree[node] = start;
else
{
int mid = (start + end) / 2;
init(array, tree, node * 2, start, mid);
init(array, tree, node * 2 + 1, mid + 1, end);
//각 구간에서 가장 높이가 낮은 것을 노드에 넣어준다
array[tree[node * 2]] < array[tree[node * 2 + 1]]
? tree[node] = tree[node * 2] : tree[node] = tree[node * 2 + 1];
}
}
//구간에서 가장 최소인 높이의 막대 인덱스 구하기
int query(vector<long long> &array, vector<long long> &tree, int node, int start, int end, int i, int j)
{
// 찾아야하는 구간과 노드구간이 겹치지 않을 때
if(end<i || start>j)
return -1;
// 찾아야하는 구간내에 노드구간이 포함될 때
else if(i <= start && end <= j)
return tree[node];
int mid = (start + end) / 2;
int leftQuery = query(array, tree, node * 2, start, mid, i, j);
int rightQuery = query(array, tree, node * 2 + 1, mid + 1, end, i, j);
// 찾는 구간이 노드구간에 포함되거나, 부분적으로 겹치는 경우
if(leftQuery == -1)
return rightQuery;
else if(rightQuery == -1)
return leftQuery;
else return array[leftQuery] < array[rightQuery] ? leftQuery : rightQuery;
}
long long getMaxArea(vector<long long> &array, vector<long long> &tree, int start, int end)
{
int N = array.size() - 1;
int idx = query(array, tree, 1, 1, N, start, end);
long long area = (end - start + 1) * array[idx];
//왼쪽 막대 존재하면 왼쪽 최대 넓이 구하기
if(start < idx)
{
long long temp = getMaxArea(array, tree, start, idx - 1);
area = max(area, temp);
}
//오른쪽 막대 존재하면 오른쪽 최대 넓이 구하기
if(idx < end)
{
long long temp = getMaxArea(array, tree, idx + 1, end);
area = max(area, temp);
}
return area;
}
int main(void)
{
ios::sync_with_stdio(0);
cin.tie(0);
while(1)
{
int N;
cin >> N;
if (N == 0)
break;
vector<long long> arr(N + 1);
for (int i = 1; i <= N; i++)
cin >> arr[i];
//세그먼트 트리 크기
int Tree_Height = (int)ceil(log2(N));
int Tree_Size = (1 << (Tree_Height + 1));
vector<long long> tree(Tree_Size);
init(arr, tree, 1, 1, N);
cout << getMaxArea(arr, tree, 1, N) << "\n";
}
return 0;
}'BOJ > 트리' 카테고리의 다른 글
| 11279번: 최대 힙 (BOJ C/C++) (0) | 2022.02.18 |
|---|---|
| 1927번: 최소 힙 (BOJ C/C++) (0) | 2022.02.18 |
| 1991번: 트리 순회 (BOJ C/C++) (0) | 2022.02.05 |
